From previous post we know that one can determine a material work function from Contact Potential Difference.
Electric potential differences are measured with voltmeters. Why not to use one to measure CPD?
To answer that a bit of explanation is in order …
How does the voltmeter work?
Voltmeter, as its name suggests, measures … electric current.
No, really?
In principle, the voltmeter measures electric current $I$ flowing through a known resistor $R$ and infers voltage $V$ from the formula
$$
V = IR.
$$
In practice, voltmeters are build like this
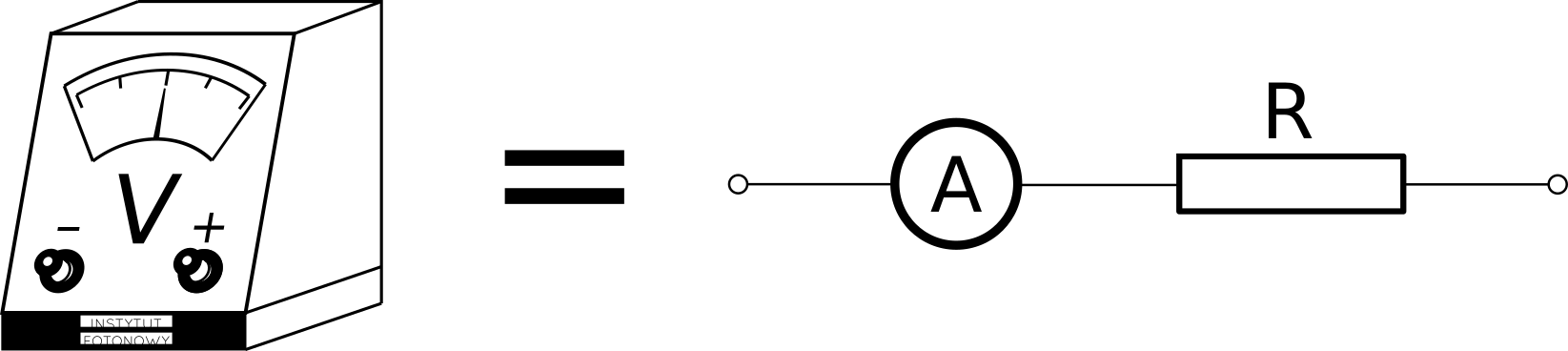
Internally, the voltmeter is just a galvanometer in series with a known resistor. In order for the voltmeter to work, some current must flow through it. The lower the current, the better the voltmeter. But the current must be there.
How not to measure CPD
As we know, the Contact Potential Difference is a voltage that shows up between two points A and B above surfaces of the connected pair of conductors like in

Hoovering probes
However, applying a voltmeter directly to points A and B
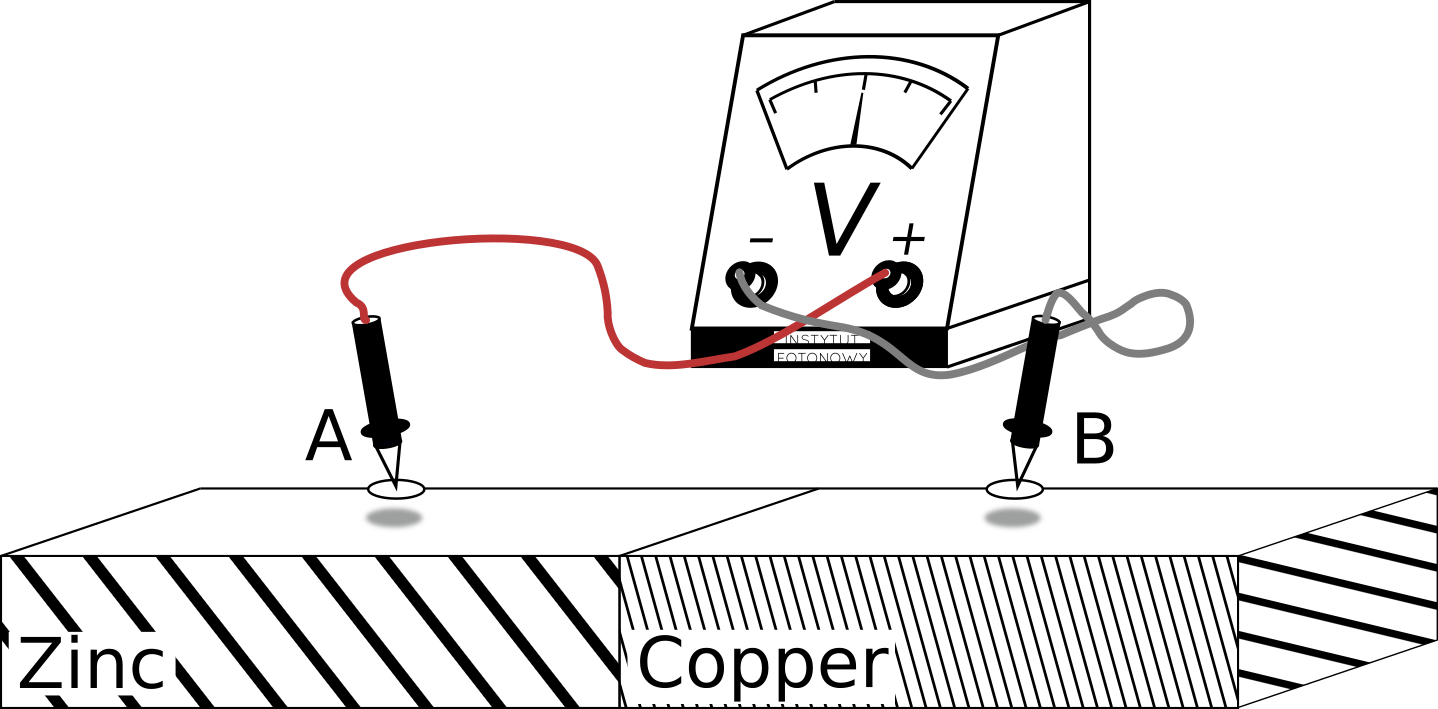
will not work. Clearly, the circuit is open and no current can flow. If there is no current flowing through the voltmeter, it will always show 0 volts.
Touching probes
If the voltmeter’s probes were touching the metal surfaces, the result will be the same but for different reason.
The electric circuit will be closed but there will be no current anyway, because both metals are in equilibrium and their Fermi levels coincide.
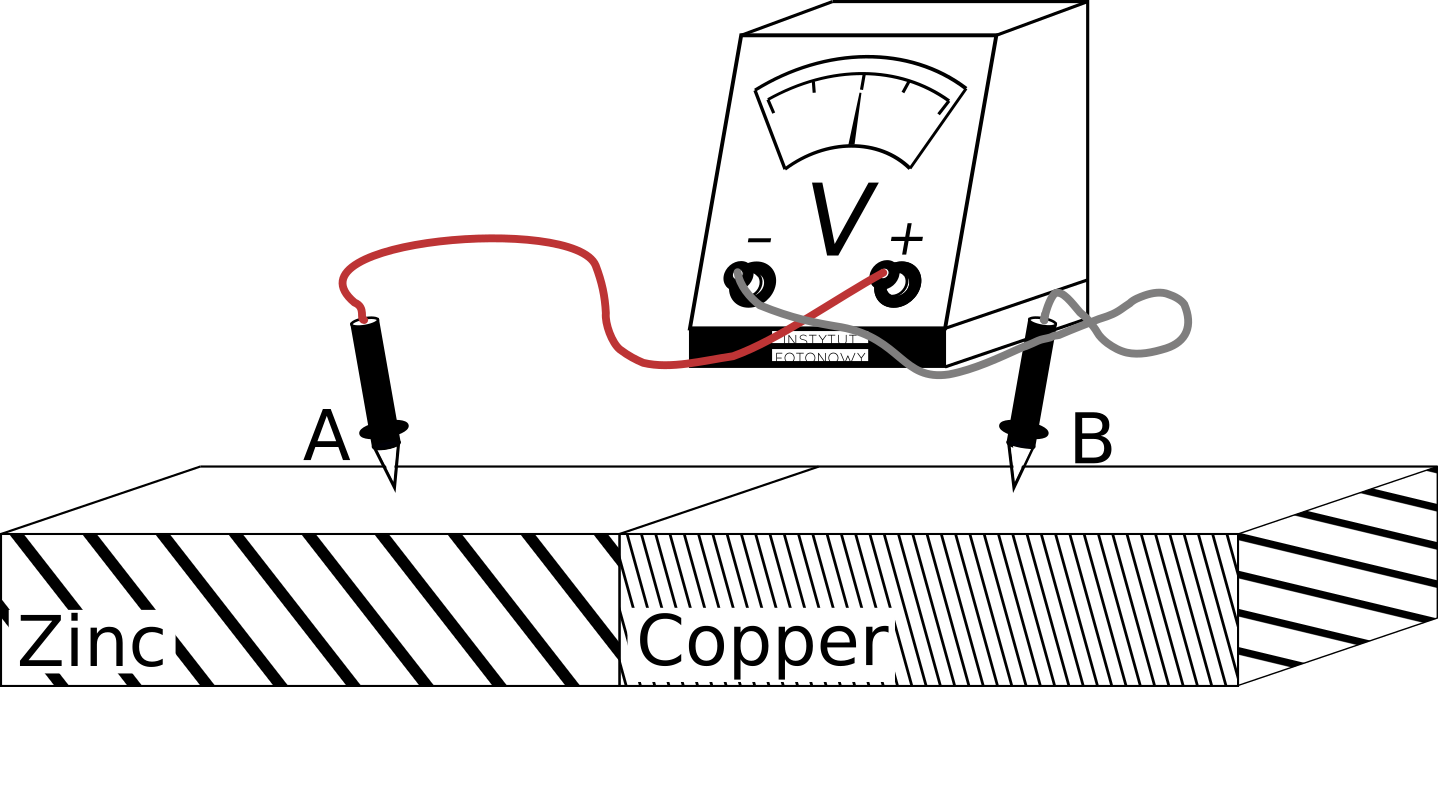
If you are amazed, how on Earth there is an electric voltage between points A and B just above the surface and it disappears between nearby points on the surface, you are hard to fool.
In fact, there is some deeper level of understanding involved: The voltmeter doesn’t show voltage but Fermi level difference $^*$.
$^*$ divided by $e$, the elementary charge constant.
No matter, above or on the surface, the electric potential difference is there.
If the probes are above the surface there is an open circuit and no DC current can flow.
If the probes are touching the surface, the electric potential difference is compensated by the difference in kinetic energy of electrons and there will be no net transfer of electrons through the voltmeter. Thus, 0 volts.
Still, how to measure the freaking CPD?!
One probe touching and one hoovering
At the risk of looking stupid, lets combine the two failed approaches
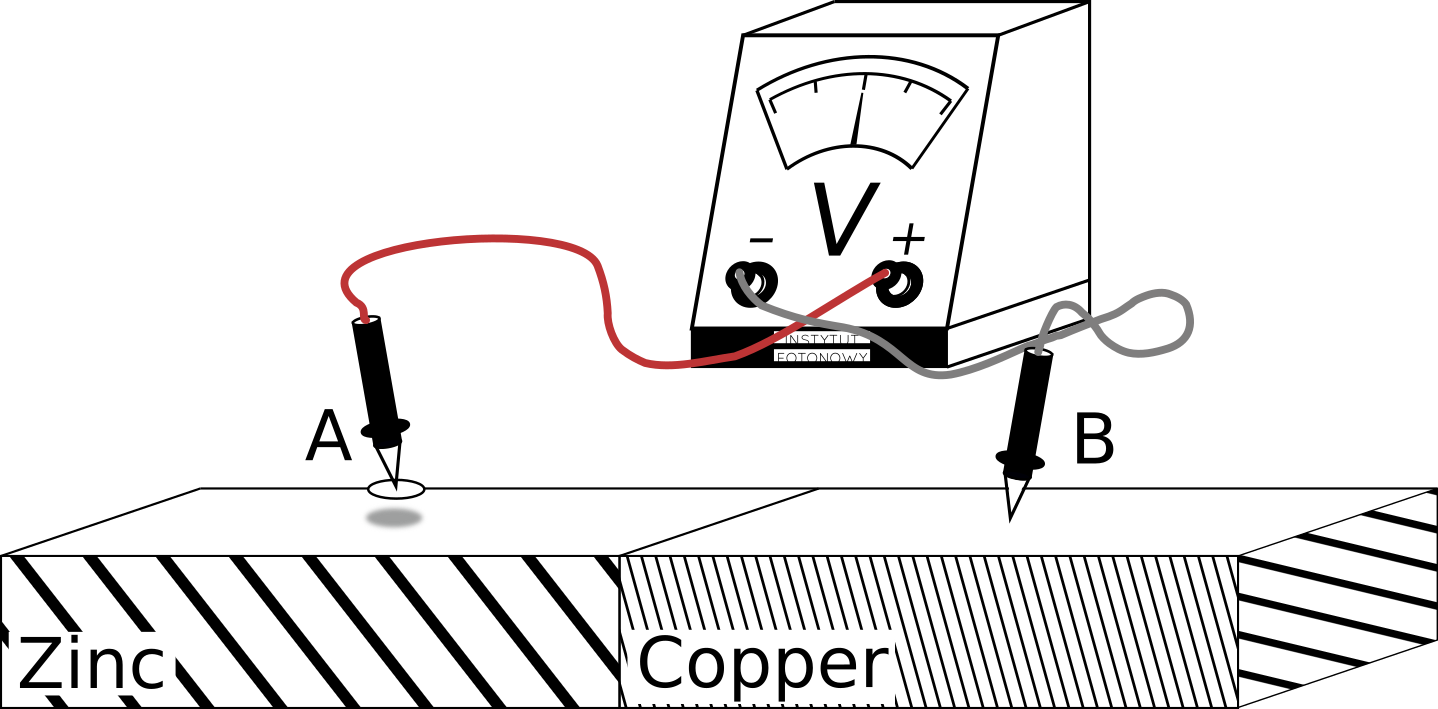
Now one probe touches the copper and another one hoovers above the zinc. Of course, the circuit is open and no current will flow. Thus the voltmeter will be quiet as before.
However, the circuit is open only for the DC current. If we managed to introduce an AC current into the circuit, it could flow. To do so, we can use the mutual capacitance between the zinc and the positive probe.

The capacitance depends on the distance between the two. If we change the distance, the capacitance will change. If the capacitance changes with fixed potential, the current will start flowing
$$
I \propto \frac{\text{d} C}{\text{d} t}.
$$
If the probe is oscillating up and down, we will get an AC current $I$. Thus, voltmeter will show the alternating voltage as well.
The capacitance between the probe and zinc is small and its changes will produce small current amplitude. The amplitude will further be dumped by the large resistor in the voltmeter. So, to improve signal quality, we need to remove the resistor 😃 .
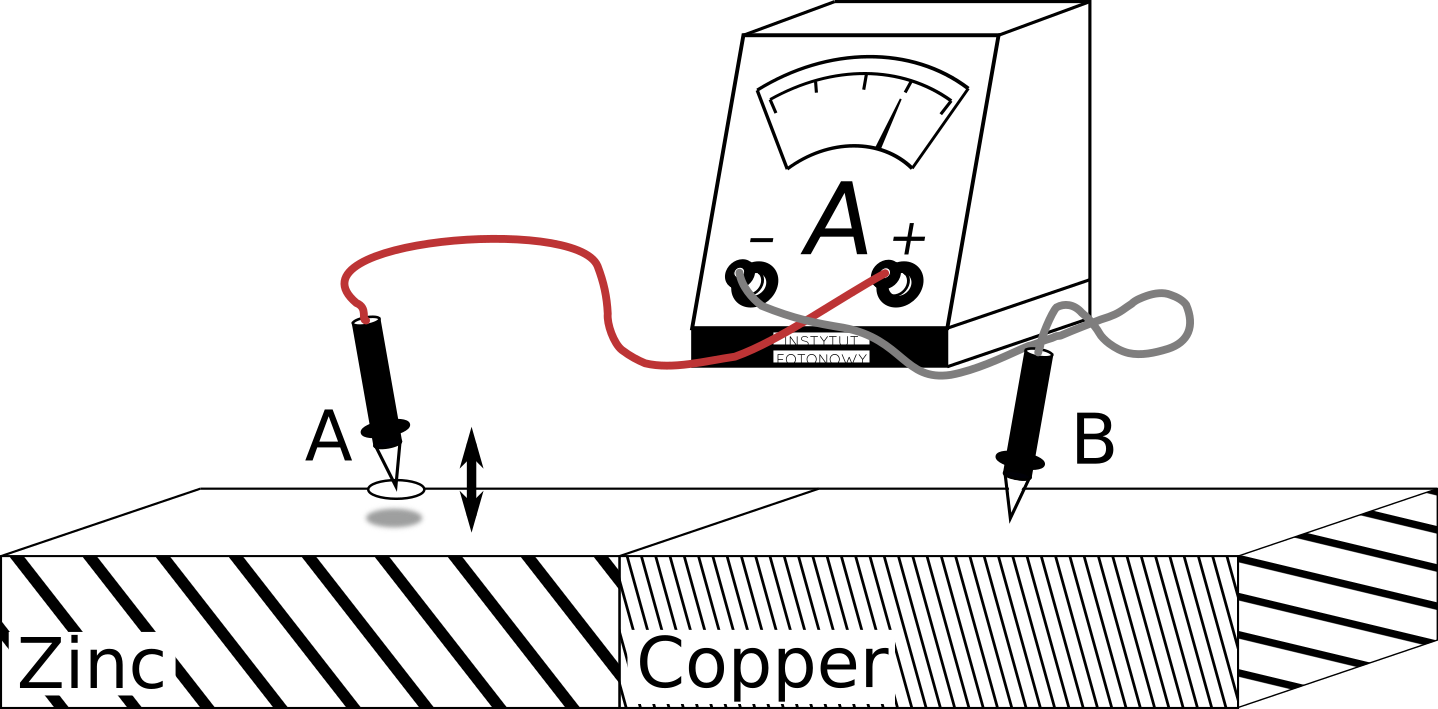
Now our voltmeter has turned into an ammeter and we can observe the AC current unimpeded.
It is all great, but how is the current related to the CPD between zinc and copper?
The sad truth is: it is not related at all. If anything, it is related to the CPD between zinc and the material the positive probe’s tip is made of.
We need to rearrange the setup.
Kelvin probe circuit
In order to explore the zinc-copper CPD we need to rebuild the setup in the following way
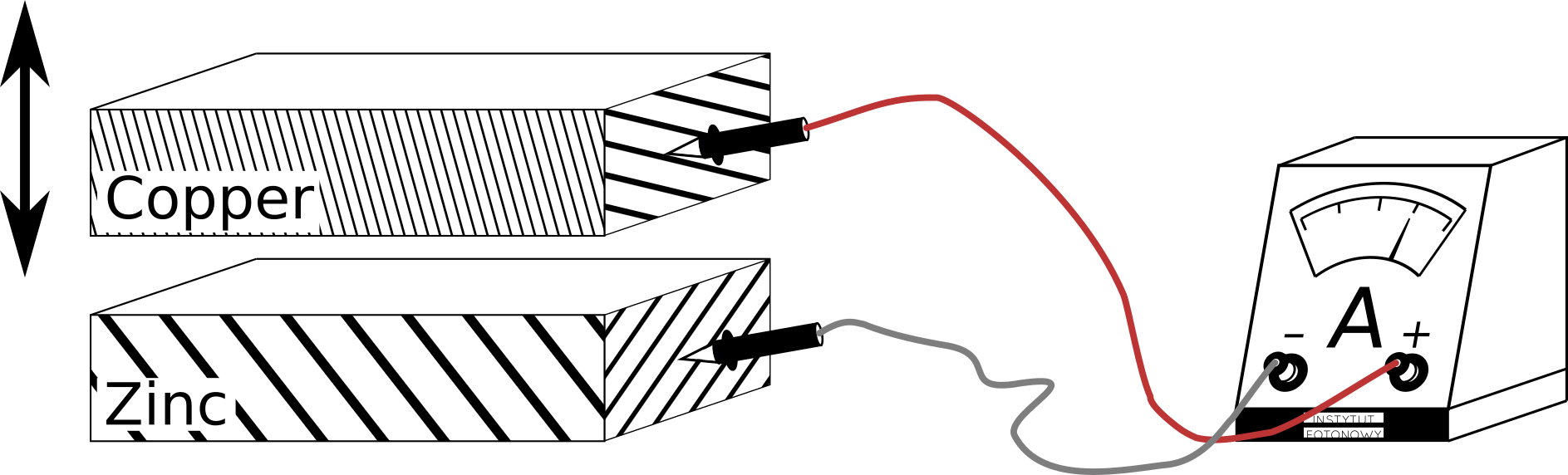
The ammeter has negligible resistance, so the two metals are still in electric contact and their Fermi levels are the same.
This time the current $I$ shown by the ammeter is proportional to the CPD of interest
$$
I = CPD \frac{\text{d}C}{\text{d}t}.
$$
In principle, the $\frac{\text{d}C}{\text{d}t}$ can be computed for simple geometries like the one above. Thus, the CPD can be determined.
In practice, it might be better to buy a Kelvin probe which works essentially the same as in the last picture, but has addressed several other issues not mentioned here.