Dark samples reflect small amount of light. Thus, the spectrometer of the MFT captures low light intensity.
This can result in noisy data. See the upper left plot in the picture below (you can click the image to enlarge):
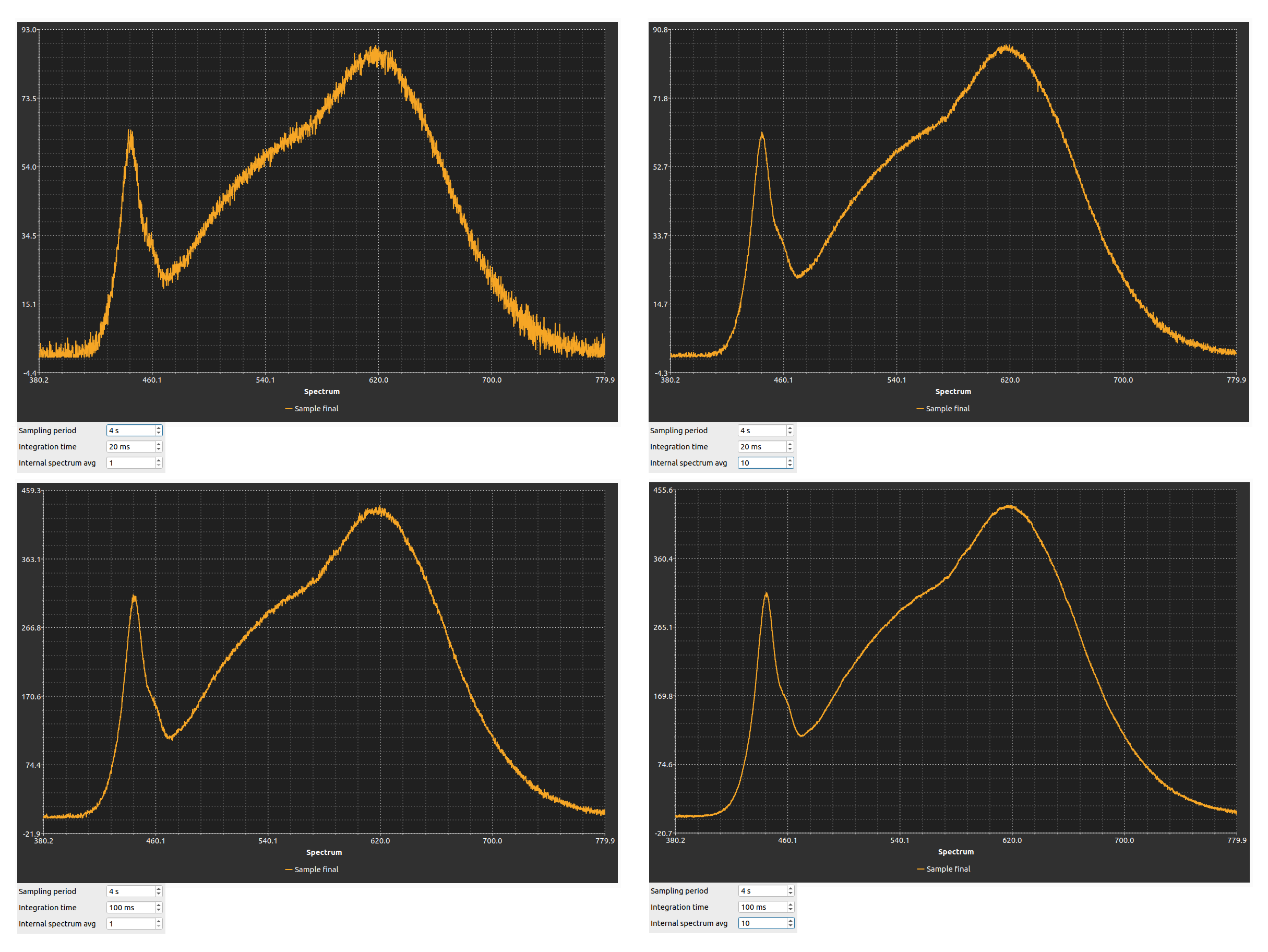
The noisy data, $s(\lambda)$, will result in the noisy aging curve. This is because the parameters of the L*a*b space relay on the reflection spectrum $R(\lambda)$ defined as
$$
R(\lambda) = \frac{s(\lambda)}{w(\lambda)},
$$
where $w(\lambda)$ is a white reference spectrum, which reflects plenty of light and usually is not noise ridden.
There are two ways to fight the noisy data problem:
- Increase the integration time (in Options) just for the dark sample and not for the white reference.
- Increase the number of averaged spectra.
The first approach will result in the smoother spectrum, see the lower left plot. Fivefold increase of the integration time should lower the relative noise roughly by factor 2. It is achieved by increase of the signal five times the original value shown in the upper left plot. The absolute noise also increases but less, about $\sqrt{5}$ times.
However, the increase in value of $s(\lambda)$ does not result in increase of $R(\lambda)$ because the software automatically takes into account relative integration times of the the signal $s(\lambda)$ and the white reference $w(\lambda)$. Actually
$$
R(\lambda) \equiv \frac{s(\lambda)/\tau_s}{w(\lambda)/\tau_w},
$$
where $\tau_s$ and $\tau_w$ are integration times for the signal and the white standard, respectively. Thus, the values of the aging curves stay on the same level, but their noise is reduced.
If one increases the number of averaged spectra, upper right plot, the absolute noise will actually decrease $\sqrt{5}$ times while keeping the values of the signal on the same level as original.
Both methods can be combined, lower right plot. This way one can keep moderate values of integration time and thus avoiding saturation of the spectrometer and still have reduced noise due to averaging.