What is I-V curve non-linearity?
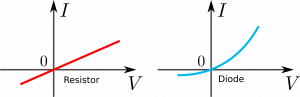
In the plots above, there are two I-V characteristics: of a resistor on the left and of a diode on the right.
The first is linear and the second is non-linear.
For any potential $V_0$, the corresponding current $I$ can be expressed as
\begin{equation}
I(V) = I(V_0) + a_1\delta V + a_2\delta V^2+a_3\delta V^3+ …,
\label{taylor_expansion}
\end{equation}
where $\delta V\equiv V-V_0$. Mathematically this is, so called, Taylor expansion of $I(V)$ at point $V_0$
The difference between linear and non-linear curve is that for linear curve
$$
a_2=a_3=a_4=…=0.
$$
If any of the parameters $a_n$ for $n\ge 2$ does not vanish, then the curve is non-linear.
The higher harmonics generation
Suppose that one would drive a linear system with a periodic potential with a single angular frequency $\omega$
$$
V = V_0 + \delta V e^{i\omega t}.
$$
Such a variation in potential will result in the following variation in the current
$$
I(V) = I(V_0) + a_1\delta V e^{i\omega t}.
$$
The current response will oscillate with the same frequency $\omega$.
However, for a nonlinear system the formula for the current is richer
$$
I(V) = I(V_0) + a_1\delta V e^{i\omega t} + a_2\delta V^2e^{i2\omega t} + a_3\delta V^3e^{i3\omega t} + …
$$
Beside the fundamental frequency $\omega$, it also contains terms with frequencies $2\omega$, $3\omega$ and more. Those extra terms are higher harmonics.
One can see, that the magnitude of the higher harmonics depends on $\delta V$ to the power of 2, 3 or more.
Thus, by reducing the amplitude of voltage oscillation, one can reduce the generation of higher harmonics.