It is easy to find formal definitions of both potentials but that does not automatically translate into understanding those concepts or grasping their significance. Here I would like to illustrate those quantities with an example that is useful in context of work functions.
Chemical and electrochemical potentials for electrons, $\mu$ and $\bar \mu$, respectively, are ubiquitous in electrochemistry and solid state physics. They are used so often that some researchers neglect the distinction and use chemical potential name for both. The convention for symbols may also lead to confusion since it is easy to drop bar over $\mu$.
To avoid even remote possibility for confusion I will refer to the electrochemical potential as Fermi level$^*$ and denote it with $E_F$ instead of $\bar\mu$
$$
E_F \equiv \bar\mu.
$$
Chemical potential
Imagine an isolated ball made of a semiconductor or metal. If the ball is electrically neutral, as in the left picture below, then the distance between its Fermi level and the lowest vaccum level is the chemical potential
\begin{equation}
\mu = E_{F}^0- E_{vac}
\label{chem_pot}
\end{equation}
where the superscript $^0$ in the $E_F^0$ denotes zero excess charge on the ball.
Electrochemical potential (Fermi level)
Now lets add some electrons to the ball. The excess negative charge, $q$, will be distributed on the ball’s surface, middle picture, and will not populate any states in the energy diagram!
Still the Fermi level of the ball will be shifted upwards. This is due to the electrostatic potential created by the excess charge. The electrostatic potential is uniform in the entire material once equilibrium is reached.
\begin{equation}
E_F = \mu - e\phi(q),
\label{echem_pot}
\end{equation}
where $\phi(q)$ is an electrostatic potential due to extra charge $q$, negative for negative $q$, and $e$ is positive elementary charge.
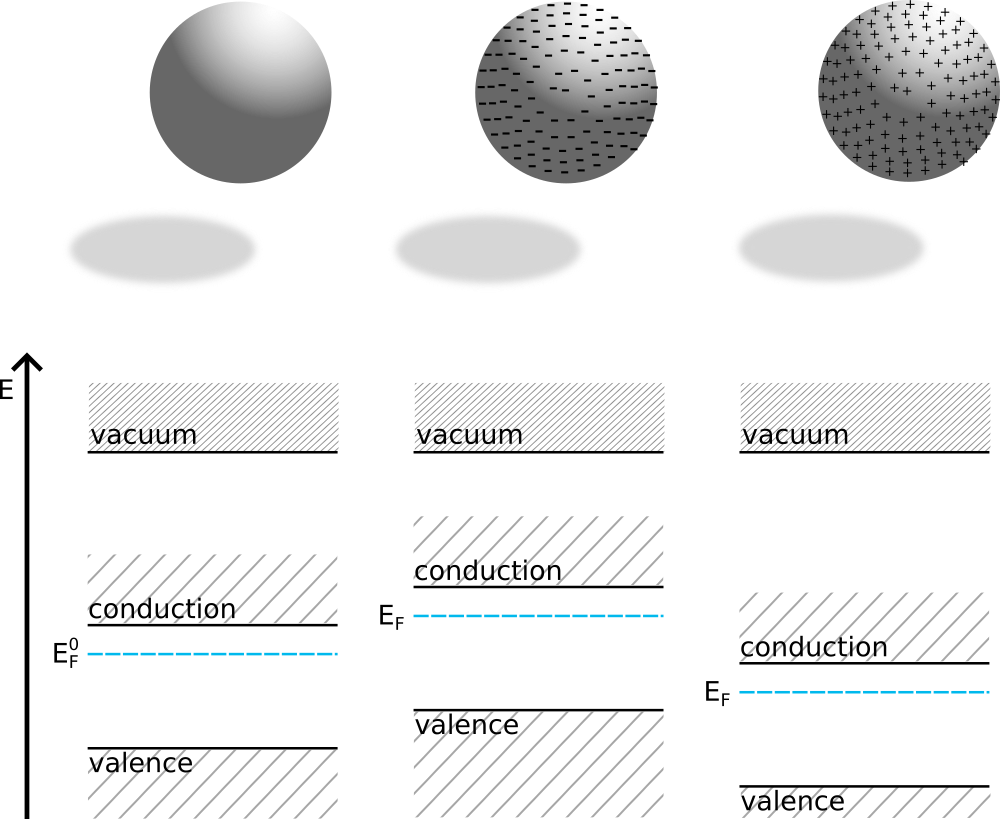
If instead of adding electrons we will extract them from the ball, it will become positively charged, $q>0$, and the Fermi level will be shifted downwards together with the material energy bands$^{**}$. The formula Eq. \ref{echem_pot} holds all the same. See the right picture.
The Fermi level enters the Fermi-Dirac function for electrons
$$
f(E) = \frac{1}{e^{(E-E_F)/k_BT}+1}.
$$
Thus, the occupation of the electronic states is not affected by the extra charges.
Two conductors in contact
When two neutral conductors are brought into an intimate contact, the equilibrium of their respective Fermi levels is achieved by redistributing electrons from the one with higher Fermi level on the surface of the one with lower Fermi level. This redistribution stops once the Fermi levels of both conductors equalize.
During the equalization process the energy bands for both materials follow the shift of respective Fermi levels, so the displaced electrons contribute to nothing more than the electrostatic potentials inside and on the surface of the conductors.
The conclusions drawn above are valid for conductors of any shape, not just balls.
Summary
The important points are:
- The chemical potential is given by Eq. $\ref{chem_pot}$
- The electrochemical potential is the same as Fermi level and is given by Eq. $\ref{echem_pot}$
- When excess charge is added to a conductor, it generates uniform electrostatic potential inside the conductor. That results in a shift of both the Fermi level and the energy bands, so there is no relative shift between them.
$^*$ As the mentioned bewilderment wasn’t enough, some people mix Fermi level with Fermi energy. Those quantities coincide only at zero temperature for which Fermi energy is defined.
$^{**}$ One may ask, so where the extracted electrons come from if not from the occupied energy levels of the ball? They do come from the occupied energy levels indeed but …
For shifts of Fermi level of order of 1 eV, it is enough to extract/add only tiny fraction of all electrons of the material. The larger the ball, the smaller the fraction. So, in most cases the change in band population of electrons can be neglected altogether.
